Diffusion in Cells
Group Meeting, November 14, 2014
Wendell Smith
Motivation
Biology
- Particles in cells do not simply diffuse
- Movement does not obey ⟨x2⟩∝t
- Highly non-Gaussian
not slope 1!
Motivation
Physics
- Just how non-gaussian can hard spheres get?
- At low density, hard spheres are perfectly gaussian
- Closer to the glass transition, they get somewhat non-gaussian
What does non-Gaussian mean?
- α2=⟨x4⟩3⟨x2⟩−1
- For a Gaussian distribution, ⟨x4⟩=3⟨x2⟩, so α2=0
What does non-Gaussian mean?
- A random walk (diffusion) is Gaussian at any given time:
- P(x,t)=12√πDte−x24Dt
- So if the particles aren't diffusing, then α2≠0
- For caged particles, α2≈−15
What does non-Gaussian have to do with the MSD?
- Short answer: its what you can't see in an MSD plot
- The MSD gives you the mean squared displacement
-
It measures the width of particle displacements of time
- α2 measures how "non-gaussian" the distribution is
Diffusion
α2=0
Mixed
α2>0
Caging
α2=−15
⟨x2⟩ and ⟨x4⟩
- MSD has a classic shape
- Almost linear for small ϕ
- Plateau region for larger ϕ
- ⟨x4⟩ looks similar to ⟨x2⟩
- N=100, monodisperse
⟨x2⟩ and ⟨x4⟩
Without the time-component
- Filled area is between
3⟨x2⟩ and ⟨x4⟩ - Area corresponds to α2: α2=⟨x4⟩3⟨x2⟩2−1
α2
- Goes up to 1.6, but no higher
- At higher densities, this is increasingly difficult to measure
- As density increases, we expect α2 to remain under 1.6
Crystallization
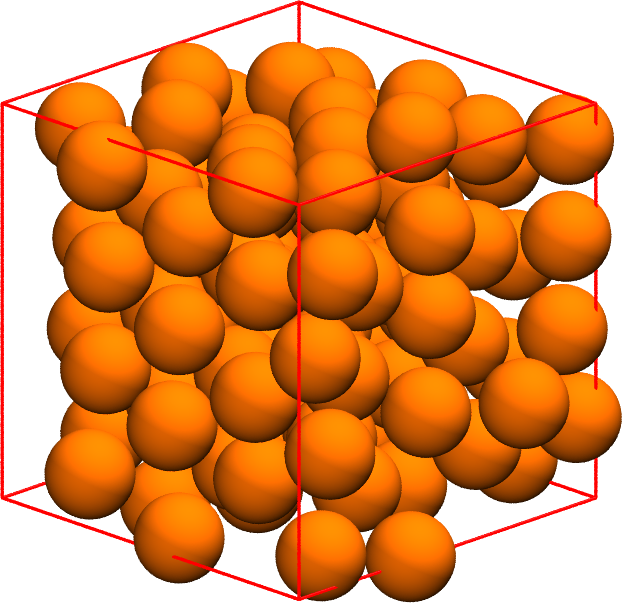
- Data shown previously included crystallization
- May switch to bidisperse
Crystallization
Characterization: Preliminary Data
- Order parameter Q6 for each simulation as a function of time
- Each simulation is its own line
- Dashed lines not included in previous data
- Some simulations started from the same initial conditions
Diffusion in Cells
Group Meeting, November 14, 2014
Wendell Smith