The Cytoplasm and
Active Matter

Wendell Smith

The Cytoplasm

Active Cells

Inactivated Cells: metabolism blocked by biochemical means

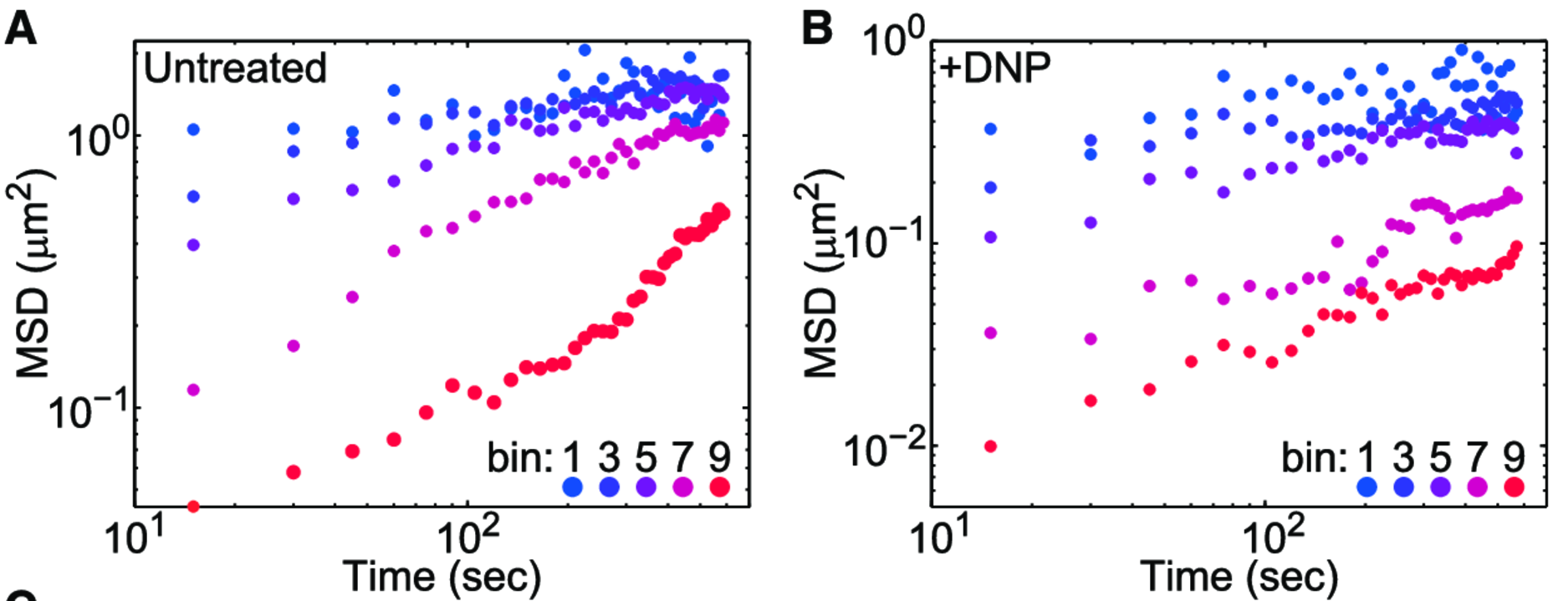
MSD of untreated vs. DNP+ cells

Particles in the cytoplasm diffuse much faster when the cell is metabolically active, by a factor of \(\sim 5-10 \)

Can metabolic “noise” lead to a difference in dynamics?

  • Cells are active, non-equilibrium systems

  • Chemical reactions are constantly consuming energy

  • Do these reactions raise the effective temperature?

Studying Active Matter

Active Matter is composed of self-driven units, active particles, each capable of converting stored or ambient free energy into systematic movement [2]

  • Active matter is an active field of research

  • Much of it is concerned with studying bird flocks, fish schools, and bacterial swarms, but occasionally considers non-living particles

  • Most studies use responsive and/or directed particles

Janus Particles

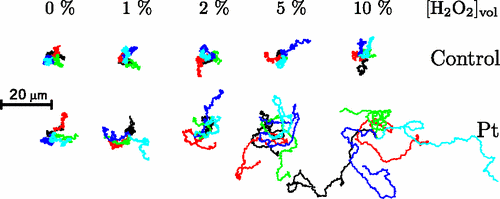
Janus Particle Trajectories
Janus Particle Trajectories in varying concentrations of H2O2

  • Half of each particle is coated with platinum, which catalyzes \(2 \mathrm{H_2 O_2 \rightarrow 2 H_2 O + O_2}\) on only one side

  • This reaction pushes the particles asymmetrically due to the local osmotic pressure gradient [1]

Janus Particles

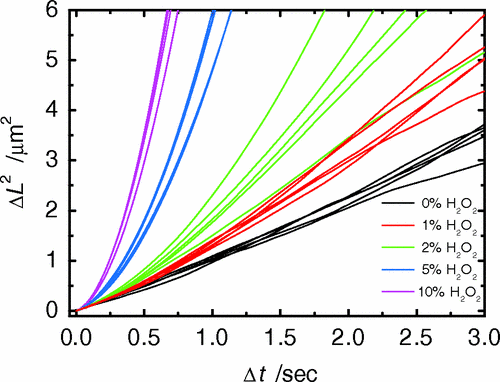
Janus Particle MSDs

  • Particles in H2O2 move much farther

\[ \begin{align*} MSD(t) &= \left< \Delta \vec r^2 \right>\\ &= \left< \vec r(t)^2 - \vec r(0)^2 \right> \end{align*} \]

Persistent Motion

  • Self-propelling particles are typically modeled with "persistent motion": propulsion along some axis of the particle

  • In eukaryotic cells, molecular motors are known to cause cytoplasm "mixing"

  • This mechanism is not expected to exist in E. coli

Biological Considerations

  • Metabolic activity does not significantly raise the temperature of the cell (right?)

  • ATP, the main energy source of metabolism, has energy \(E_\mathrm{ATP} \sim 20 k_B T\)

  • Metabolic activity would not have a rotational orientation

Simulating Metabolism

  • Langevin thermostat \[ \vec F = -\vec \nabla U - \gamma \vec v + \vec \Gamma_T + \vec \Gamma_k\left(t\right) \]

    • WCA potential / repulsive Lennard-Jones for \(U\)

    • Damping \(\gamma\) to simulate solution viscosity

    • Random, instantaneous "kicks" to the particles

      • \(\vec \Gamma_T\) for the thermostat; balanced by \(\gamma\)

      • \(\vec \Gamma_k\) for metabolism

Random Kicks

ThermostatMetabolism

  • \(\Gamma_T \sim \Delta t k_B T \sim {10}^{-5} k_B T\)

  • Every timestep

  • Correlated: satisfy FDT

  • Gaussian distribution

  • Balanced by \(-\gamma \vec v\)

  • \(0 \le E_k \le 20 k_B T\)

  • Instantaneous

  • Infrequent, ~100—1000 timesteps

  • Uncorrelated

  • Uniform distribution

Simulation

Without Activity

With Activity

Considerations

\(\phi\)

the packing fraction

\(T_0\)

the thermostat temperature

\(\gamma\)

the thermostat damping rate

\(E_k\)

the kick magnitude

\(f_k\)

the kick frequency

  • If \(f_k E_k \ll \gamma T_0\), then the thermostat can keep \(T \sim T_0\)

Simulation

MSDs with Activity

  • \(f\) is the kick frequency, T is the measured temperature

  • Kicks that are too frequent raise the temperature

Simulation, Larger Kicks

MSDs with Activity

  • \(f\) is the kick frequency, T is the measured temperature

  • Kicks that are too frequent raise the temperature

Acknowledgments

  • Corey O’Hern, Mark Shattuck, Christine Jacobs-Wagner

  • Brad Parry, Ivan Surovtsev, Eric Dufresne, and everyone I talked to

  • Sackler, PEB, and HHMI

Bibliography

  1. J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh, and R. Golestanian, Phys. Rev. Lett. 99, 048102 (2007).

  2. M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao, and R. A. Simha, Rev. Mod. Phys. 85, 1143 (2013).